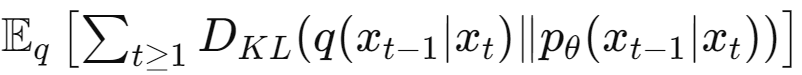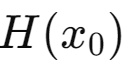[KUBIG; Basic-CV] About Diffusion Model

Reference: Denoising Diffusion Probabilistic Model
Denoising Diffusion Probabilistic Models
We present high quality image synthesis results using diffusion probabilistic models, a class of latent variable models inspired by considerations from nonequilibrium thermodynamics. Our best results are obtained by training on a weighted variational bound
arxiv.org
1. Introduction
Diffusion Probabilistic Model
Variational inference를 사용하여 일정 시간 후 데이터와 일치하는 샘플을 생성하도록 훈련된 parameterized Markov chain. 신호가 완전히 파괴될 때까지 데이터를 역방향으로 점진적으로 노이즈를 추가하는 Markov chain을 역으로 학습.
만약 Diffusion이 소량의 Gaussian noise을 갖고 있다면, 샘플링 체인 전환을 conditional Gaussians로 설정하면 신경망 파라미터화를 단순화할 수 있음.
Variational Inference
복잡한 확률 모델에서 정확한 추론이 어려운 경우에 근사 추론을 수행하기 위한 방법, 목표는 계산하기 어려운 후방 분포(posteriors)를 보다 간단한 분포로 근사하여, 이 근사 분포를 최적화하는 것
Parameterized Markov Chain
Markov Chain은 상태 전환이 현재 상태에만 의존하는 확률 모델을 의미하는데, Parameterized은 이러한 상태 전환 확률이 학습 가능한 파라미터에 의해 정의된다는 것을 의미. 즉, 모델은 데이터를 통해 이 전환 확률을 학습하여, 이후에 새로운 데이터를 생성하거나 기존 데이터를 샘플링하는 데 사용
Gaussian Noise
통계적으로 평균이 0이고 분산이 1인 정규 분포를 따르는 노이즈를 의미. 데이터에 노이즈를 추가하는 방법 중 하나로, 이는 많은 자연 현상에서 발생하는 랜덤 변동을 모델링하는 데 유용
Efficiency and Quality
- 모델의 특정 파라미터화는 training 중 여러 노이즈 레벨에 대한 denoising score matching 및 샘플링 중 annealed Langevin dynamics와의 동등성을 보여줌
- Diffusion model의 log likelihoods는 다른 likelihood-based models와 경쟁하지 못하고 에너지 기반 모델과 score matching에 대한 annealed importance sampling의 큰 추정치보다는 더 나은 성능을 보임.
- 모델의 Lossless Codelengths 대부분은 지각할 수 없는 이미지 세부 사항을 설명하며, 이는 손실 압축과 유사. Diffusion models의 샘플링 절차는 progressive decoding 과 유사하며, autoregressive decoding과 유사하지만 더 일반화된 순서 기능을 갖추고 있음
Annealed Langevin Dynamics
샘플링 기법 중 하나로, 특히 확률 밀도 함수를 최적화하는 데 사용. Langevin dynamics는 확률적 미분 방정식 (SDE)을 기반으로 샘플을 생성하는 방법이며, 물리학에서 입자의 움직임을 모델링하는 데 사용되며, 머신 러닝에서는 확률 분포에서 샘플을 생성하는 데 응용. Annealing은 차적으로 시스템의 온도를 낮추어 에너지 상태를 안정화하는 과정을 말하는데, 이 과정에서 노이즈를 점차 줄여가며 샘플을 생성하여, 더 정확한 샘플을 얻을 수 있음
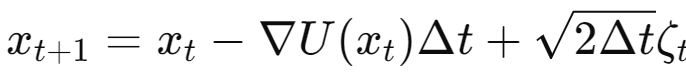
- $x_t$: 시점 t에서의 상태
- $\nabla{U(x_t)}$: 상태 $x_t$에서의 에너지 함수 $U(x)$의 gradient
- $\Delta{t}$: 시간 스텝
- $\varsigma_t$: 평균이 0이고 분산이 1인 가우시안 노이즈
Energy-Based Model
확률 분포를 직접 모델링하지 않고, 데이터의 에너지 함수를 정의하여 간접적으로 모델링하는 방법으로 데이터의 각 상태에 대해 스칼라 값을 할당하며, 낮은 에너지 값을 가지는 상태가 높은 확률을 갖게 됨.
Annealed Importance Sampling
샘플링 기법으로, 샘플링 분포와 목표 분포가 다를 때 사용. 샘플링 과정에서 Annealing 기법을 적용하여, 샘플의 중요도를 점진적으로 조정하면서 목표 분포에 더 가까운 샘플을 생성하는 방법. 특히 에너지 기반 모델과 같은 복잡한 분포에서 샘플을 효율적으로 얻는 데 사용
Lossless Code
데이터 압축에서 원래 데이터를 전혀 손실하지 않고 그대로 복원할 수 있는 압축 방법 (png, zip).
Progressive Decoding
처음에는 대략적인 정보를 제공하고, 점차 세부 정보를 추가하여 점진적으로 전체 데이터를 복원. 특히 이미지나 비디오 스트리밍에서 자주 사용되며, 초기에는 저해상도 버전을 제공하고 시간이 지남에 따라 고해상도로 전환.
Autoregressive Decoding
시퀀스 데이터를 디코딩할 때, 이전에 생성된 항목을 기반으로 다음 항목을 예측하는 방법. 순차적 데이터 생성에 매우 효과적
2. Background
(1) Joint Distribution

위 식은 $x_0$부터 $x_T$까지의 잠재 변수의 전체 확률 분포를 정의, $p(x_T)$는 최종 상태 $x_T$의 분포,
$\prod_{t=1}^{T} p_{\theta}(x_{t-1}|x_t) $는 각 시점 $t$에서 $x_t$로 부터 $x_{t-1}$을 샘플링하는 조건부 확률 분포를 곱한 것 역전파 과정(reverse process)을 나타냄 => 노이즈를 제거하여 원래 데이터를 복원하는 과정

위 식은 역방향 과정에서의 조건부 확률 분포를 정의. $p_{\theta}(x_{t-1}|x_t)$는 $x_t$가 주어졌을 때 $x_{t-1}$의 확률 분포를 나타냄. 이 분포는 가우시안 분포 N으로 표현되며, 각각 위와 같은 평균과 공분산을 갖게되며, 평균과 공분산 모두 모델 파라미터 $\theta$에 의해 학습 됨
(2) Forward Process

위 식은 정방향 과정 (forward process) 또는 확산 과정 (diffusion process)을 정의.
$q(x_{1:T}|x_0)$는 초기 상태에 시작하여 최종 상태에 도달하는 확률 분포, $\prod{q}$는 각 시점 $t$에서 $x_{t-1}$에서 $x_t$로의 조건부 확률을 곱한 것 => 점진적으로 노이즈를 추가하는 과정
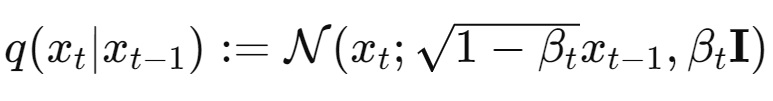
위 식은 forward process에서의 조건부 확률 분포를 정의하며, $\beta_t$는 각 시점 $t$에서의 노이즈 수준을 나타내는 파라미터이며 공분산 행렬 $\beta_tI$는 노이즈가 독립적이고 등분산임을 의미
(3) Variational Bound on Negative Log Likelihood
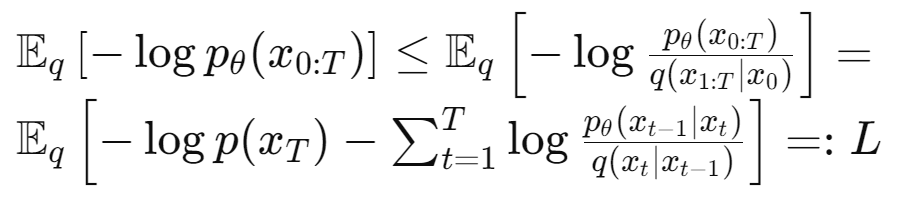
위 식은 Variational Inference의 주요 목표인 negative log likelihood의 Variational Bound를 나타냄
최종적으로 얻어진 식 $L$은 모델 $p_\theta$와 근사 분포 $q$ 간의 Kullback-Leibler divergence를 최소화하는 것을 목표로함
Variational Bound
Variational Inference에서는 posterior distribution $p(z|x)$를 직접 계산하는 대신, 비교적 간단한 분포 q(z)를 사용하여 근사하고, 두 분포 사이의 차이를 최소화하는 것이 목표 => 이때 사용하는 척도가 Kullback-Leibler divergence. 또 이 KL을 최소화 하기 위해 사용하는 것이 Variational Bound로 Evidence Lower Bound (ELBO)로 표현됨.

(4) Reparameterization of Forward Process
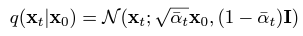
위 식은 정방향 과정의 분포를 재파라미터화 하여 정방향 과정에서 임의의 시점 $t$에서 $x_0$ (원래 데이터)로부터 $x_t$ (노이즈 추가된 데이터)를 샘플링 할 수 있도록 함. ($\sqrt{\bar{\alpha_t}}x_0$ 가 posterial mean에 해당)

(5) Variance Reduction using KL Divergence

위 식은 KL divergence를 사용하여 분산을 줄이는 방법. 각 시점 $t$에서의 KL divergence를 계산하여 샘플링 과정의 분산을 줄이고, stochastic gradient descent을 통해 효율적인 학습을 가능하게 함.
또, 이는 Rao-Blackwellized 방식으로 계산될 수 있어, 고분산의 Monte Carlo 추정치 대신 닫힌 형태의 식으로 표현됨.
Kullback-Leibler (KL) 발산
두 확률 분포 간의 차이를 측정하는 비대칭적인 척도로 참 분포 P와 이를 근사하는 분포 Q 사이의 차이를 계산

여기서, $log\frac{P(x)}{Q(x)}$는 $x$에서의 정보 이득을 나타냄
(6) Conditional Distribution of $x_{t-1}$, (7) Simplified KL Divergence

위 식들은 특정 시점 $t$에서 $x_t$와 $x_0$를 조건으로 하는 $x_{t-1}$의 조건부 분포를 나타내어 정방향 과정에서 샘플링을 단순화하고, 효율적인 계산을 가능하게 함.
posterior mean (\tilde{\mu})
베이즈 추론에서 사용되는 용어로, 주어진 관측 데이터에 대한 조건부 확률 분포의 평균을 의미
$P(\theta|x) = \frac{p(x|\theta)p(\theta)}{p(x)}$
θ: 잠재변수 또는 파라미터
x: 관측된 데이터
p(θ|x): posterior distribution (후방 분포)
p(x|θ): likelihood
p(θ): prior distribution (사전 분포)
p(x): evidence 또는 marginal likelihood로, 주어진 데이터에 대한 전체 확률
=> $E(\theta{|x})d\theta$
3. Diffusion models and denoising autoencoders
(1) Forward process and $L_T$
Forward process는 잠재 변수 $x_0$에서 시작하여 단계별로 노이즈를 추가해가며 최종 상태 $x_T$에 도달하는 과정.
위 식 (2)에서 $\beta_t$는 reparameterization를 통해 학습할 수 있으나 여기서는 이를 일정한 상수로 고정 => 학습 과정에서 후방 분포 $q$에는 학습할 파라미터가 없으므로 $L_T$는 일정한 값으로 간주되어 무시할 수 있음
(2) Reverse process and L_{1:T-1}
역방향 과정은 각 시점 $x_t$에서 $x_{t-1}$로의 전환을 모델링
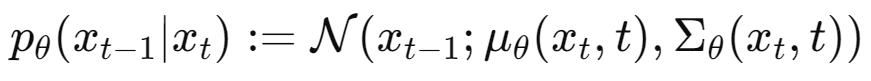
이때, 평균과 분산은 모델 파라미터 $\theta$에 의해 학습됨.
실험적으로 분산을 training 되지 않은 시간 의존 상수 $\sigma_t^2I$로 설정.
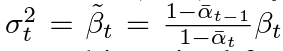
평균을 나타내기 위해 forward process posterior mean을 예측하는 모델을 제안 (parameterization of $\mu_\theta$ is a model that predicts $\tilde{\mu}_t$)
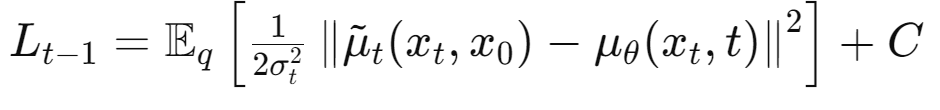
식 (4) reparameterizing
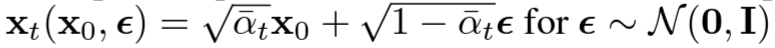
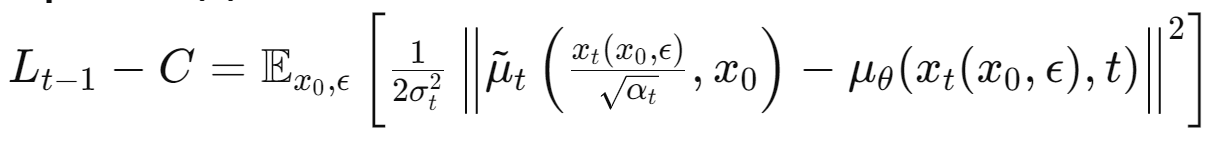
$x_t(x_0, \epsilon)$는 노이즈 $\epsilon$와 초기상태 $x_0$에 의해 생성된 $x_t$
=> $\mu_\theta(x_t, t)$가 $\tilde{\mu}_t$와 유사하도록 학습해야 한다!

=> 입력 $x_t$와 노이즈 $\epsilon$를 이용하여 $\mu_\theta$를 구하고, must predict $\frac{1}{\sqrt{\alpha_t}}(x_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}_t}}\epsilon)$
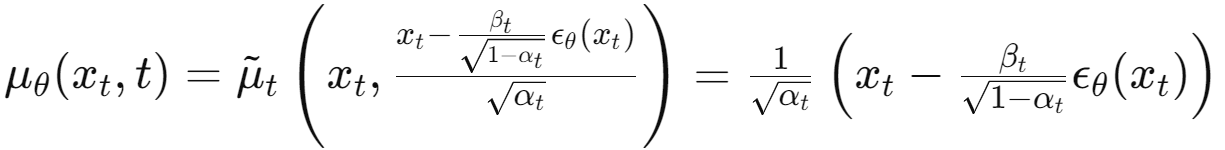
=> $\mu_\theta$는 모델이 $x_t$와 노이즈 $\epsilon_\theta(x_t)$를 사용하여 예측해야 하는 값

이 식은 다중 노이즈 레벨에서의 denoising score matching을 나타내며, Langevin-like reverse process의 변형을 최적화하는 목적과 동일하다는 것을 보여줌
Summary
(a) 역방향 과정 평균 함수 학습
- $\mu_\theta$는 역방향 과정에서 $x_t$로부터 $x_{t-1}$을 예측하는 평균 함수
- 이 평균 함수는 $\tilde{\mu}_t$를 예측하도록 학습할 수 있음
(b) $\epsilon$ 예측 Parameterizing
- 모델의 Parameterizing 변경하여 $\epsilon$을 예측하도록 학습할 수도 있지만 실험 결과, $\epsilon$을 예측하는 Parameterizing이 초기 샘플의 품질을 더 악화시키는 것으로 나타남
- $\epsilon$ 예측 Parameterizing은 Langevin dynamics와 유사하며, Variational Bound를 denoising score matching과 유사한 목표로 단순화 함.
- 이는 모델이 노이즈 제거 과정에서 더욱 효과적으로 학습할 수 있도록 도움
(c) 다른 Parameterizing
- $\mu_\theta(x_t,t)$를 $\tilde{\mu}_t$로 예측하거나, $\epsilon$을 예측하는 것은 단순히 $p_\theta(x_{t-1}|x_t)$의 다른 Parameterizing일 뿐 => section 4에서 확인해보기!
(3) Data Scaling, Reverse Process Decoder, and $L_0$
Data Scaling
이미지 데이터는 {0,1,…,255}\{0, 1, \ldots, 255\}의 정수로 구성되어 있으며, 이를 [−1,1][-1, 1] 범위로 선형 스케일링 → 이렇게 하면 역방향 과정에서 일관되게 스케일된 입력을 사용하여 표준 정규 분포 p(xT)p(x_T)에서 시작할 수 있음
Reverse Process Decoder, and $L_0$
discrete log likelihoods를 얻기 위해 역방향 과정의 마지막 항을 독립적인 discrete decoder로 설정하고 이 decoder은 가우시안 분포로부터 유도됨

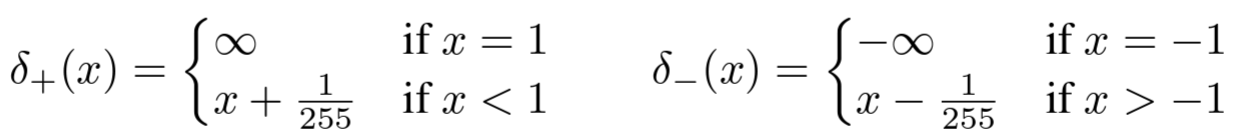
(4) Simplified Training Objective
기존의 Variational Bound (VB)는 역방향 과정과 디코더를 정의하면서 VB는 Equ. (12), (13)에서 유도된 항으로 구성되며, 이 VB는 파라미터 $\theta$에 대해 명확하게 미분 가능하므로, 이를 사용하여 모델을 훈련할 수 있지만, 샘플 품질을 향상시키고 구현을 단순화하기 위해, VB의 변형된 버전을 사용하여 모델을 훈련.
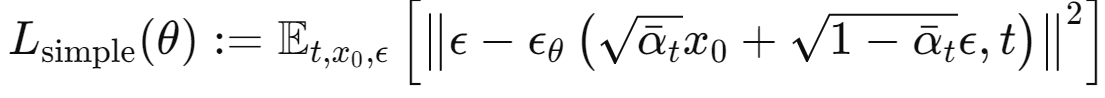
여기서 $t$는 1과 T 사이의 균등 분포에서 샘플링되며, t=1인 경우, Equ(13)의 discrete decoder 정의에서 적분과 가우시안 확률 밀도 함수의 곱으로 근사되고 t>1인 경우는 Equ(12)의 가중치가 없는 버전에 해당
위 단순화된 objective의 장점은 Equ(12)에서의 가중치를 버려 표준 VB와 비교하여 복원의 다른 측면을 강조 ( 더 어려운 노이즈 제거 작업에 집중하도록 유도하고, 모든 시간 스텝에서 균형 잡힌 학습 가능)하며 작은 t 값은 노이즈가 매우 적기 때문에, 네트워크가 더 어려운 denoising 작업에 집중할 수 있도록 함.
Training & Sampling Algorithm

| Algorithm 1; Training | Algorithm 2; Sampling |
| (1) Repeat (2) Data Sampling 사전분포 $q(x_0)$로부터 원본 데이터 $x_0$를 샘플링 (~) (3) Time Step Sampling 1부터 T까지의 균등 분포에서 시간 스템 t를 무작위로 선택 (4) Noise Sampling 평균이 0이고 분산이 1인 가우시안 분포로부터 노이즈 $\epsilon$ 샘플링 (5) Gradient Descent 모델 파라미터 $\theta$를 위와 같은 손실함수를 최소화하도록 업데이트 (6) 수렴할 때까지 반복 |
(1) 초기 상태 Sampling 평균이 0이고 분산이 1인 가우시안 분포로부터 초기 상태 $x_T$를 샘플링 (2) 역방향 시간 스텝 반복 t = T, ..., 1 동안 반복 (3) 노이즈 샘플링 - $t>1$: $z ~ N(0, I)$: 평균이 0이고 분산이 1인 가우시안 분포로부터 초기 상태 $x_t$를 샘플링 - $t=1$: $z=0$으로 마지막 스템에서는 노이즈 추가 X (4) 상태 $x_{t-1}$을 위와 같이 업데이트 이때, $\epsilon_\theta(x_t, t)$는 모델이 예측한 노이즈 (5), (6) 모든 시간 스텝 완료할 때까지 반복하고 최종상태 (노이즈가 제거된 원본 데이터) $x_0$를 반환 |
4. Experiments
(1) Sample Quality
- CIFAR10 데이터셋을 사용
- FID, Inception 점수, log likelihoods(loss less code lengths) 계산
(1) FID (Frechet Inception Distance)
생성된 이미지와 실제 이미지 간의 통계적 차이를 측정하여 두 데이터 분포의 유사성을 평가
두 데이터셋의 피처 벡터(주로 Inception V3 네트워크의 중간 레이어에서 추출된)를 에 대해 평균과 공분산을 계산하여 Frechet 거리를 계산하고, 작을수록 더 좋은 품질의 이미지
=> 두 데이터 분포의 유사성을 측정하므로, 단순히 픽셀 간의 차이를 측정하는 것보다 더 의미 있는 결과를 제공

여기서 $\mu_x, \mu_g$는 실제 이미지와 생성된 이미지의 평균 벡터, $\Sigma_x, \Sigma_g$는 실제 이미지와 생성된 이미지의 공분산 행렬, $Tr$는 행렬의 대각합(Trace)를 의미
(2) Inception Score (IS)
생성된 이미지를 Inception V3 네트워크에 입력하여 클래스 확률 분포 $p(y|x)$를 얻고 모든 이미지에 대한 클래스 확률 분포 $p(y)$를 계산. 두 분포 간의 KL 발산을 계산하여 Inception Score를 얻음.
=> 높을수록 더 좋은 품질의 이미지를 나타내고 이미지의 품질과 다양성을 모두 고려하여 실제 이미지와 비교하지 않고 생성된 이미지의 자체 품질을 평가
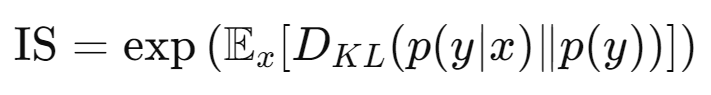
(3) Negative Log-Likelihood (NLL)
모델이 데이터를 얼마나 잘 설명하는지를 측정하는 지표. 데이터 $x$에 대해 모델이 예측한 확률 분포 $p_\theta(x)$를 계산하고 log likelihood $-logp_\theta(x)$를 계산하여 데이터가 모델의 예측 분포에 얼마나 잘 맞는지를 평가
(2) Reverse process parameterization and training objective ablation
- 기본 옵션인 $\tilde{\mu}$를 에측하는 것은 VB에서만 잘 작동하며, 단순화된 MSE에서는 잘 작동하지 않음
- 역방향 과정의 분산을 학습하는 것은 (파라미터화된 대각 행렬 $\Sigma_\theta{(x_t)}$를 VB에 포함) 불안정한 학습과 더 낮은 샘플 품질로 이어짐
- 즉! $\epsilon$을 예측하는 것은 단순화된 목표를 사용하여 학습할 때 훨씬 더 나은 성능 보임
- 모든 실험에서 T=1000으로 설정, 정방향 과정의 분산 $\beta_t$는 $\beta_1 = 10^{-4}$에서 $\beta_T = 0.02$까지 선형적으로 증가하는 상수로 설정 (이 상수는 [-1, 1]로 scaled data에 대해 작게 유지되어 역방향과 정방향 과정이 유사한 함수 형태를 가지면서도 $x_T$에서의 SNR을 최대한 작게 유지)
- 역방향 과정을 표현하기 위해 U-Net 백본을 사용하고 이 네트워크는 그룹 정규화(group normalization)를 사용하며, 시간에 따라 파라미터가 공유됨
- Transformer의 sine positional embedding과 16x16 feature map 해상도에서의 self attention을 사용
(3) Progressive Coding

| Algorithm 3; Sending $x_0$ | Algorithm 4; Receiving |
| (1) 초기 상태 전송 $x_T ~ q(x_T|x_0)$를 모델 p(x_T)를 사용하여 전송 ($x_T$는 노이즈가 추가된 상태) (2) 역방향 시간 스텝 반복 $t = T-1, ..., 2$ 동안 반복 (3) 중간 상태 전송 각 시간 스텝 t에서 $x_t ~ q(x_t|x_{t+1}, x_0)$를 모델 $p_\theta(x_t|x_{t+1})$를 사용하여 전송 (4), (5) 모든 시간 스텝을 완료할 때까지 반복하고 최종적으로 $x_0$를 모델 $p_\theta(x_0|x_1)$를 사용하여 전송 |
(1) 초기 상태 수신 $x_T$ 모델 $p(x_T)$를 사용하여 수신 (2) 역방향 시간 스텝 반복 $t = T-1, ..., 2$ 동안 반복 (3) 중간 스텝 수신 각 시간 스텝 $t$에서 $x_t$를 모델 $p_\theta(x_t|x_{t+1})$를 사용하여 수신 (4), (5) 모든 시간 스텝을 완료할 때까지 반복하고 최종적으로 $x_0$를 반환 |
Codelength
Entropy
주어진 확률 분포에서 발생할 수 있는 불확실성 또는 정보량을 측정하고, 엔트로피가 높을수록 데이터의 불확실성이 크며, 이를 효율적으로 표현하기 위해 더 많은 비트가 필요
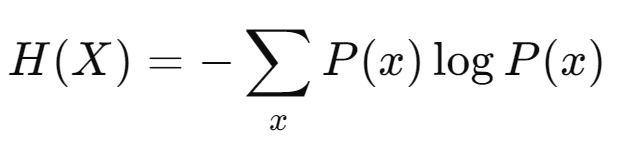
Codelength
특정 데이터나 사건을 압축하여 표현하는 데 필요한 비트의 수를 의미, 엔트로피가 낮을수록 더 짧은 코드 길이로 데이터를 표현할 수 있음
최적 코드
발생 확률이 높은 데이터 항목은 더 짧은 비트로, 발생 확률이 낮은 항목은 더 긴 비트로 표현
=> 평균 코드 길이 ($l(x)$는 x의 코드 길이)
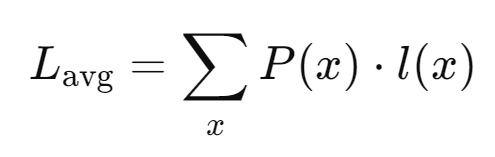
Variational Bound & Codelength
확률 모델에서는 데이터 분포를 근사하는 모델을 학습하는데 데이터를 얼마나 잘 설명하는지 평가하기 위해, 데이터를 압축할 때 필요한 평균 코드 길이를 사용
- 손실 없는 압축: 모든 데이터를 원래 형태로 복원할 수 있는 압축 방식
- 손실 압축: 데이터의 일부를 손실하더라도, 중요한 정보를 유지하면서 데이터를 압축
- training, testing 간의 차이는 최대 0.03 bits per dimension => overfitting되지 않았음을 시사 (training/test data를 각각 처리할 때 codelength가 차이가 적다는 것은 overfitting되지 않았다는 것)
- lossless codelength 측면에서 annealed importance sampling을 사용한 score matching보다 나은 성능을 보이지만, 다른 유형의 likelihood-based 생성 모델들과 비교해서는 경쟁력이 떨어짐
Lossy Compression
Rate
데이터를 압축할 때 필요한 평균 비트 수를 의미, 데이터 압축의 효율성을 나타내는 지표
Distortion
압축된 데이터를 원래 데이터로 복원할 때 발생하는 정보 손실 (MSE)을 의미.
Rate-Distortion Theory
주어진 허용가능한 왜곡 수준에서 압축할 수 있는 최소 비율을 찾는 문제
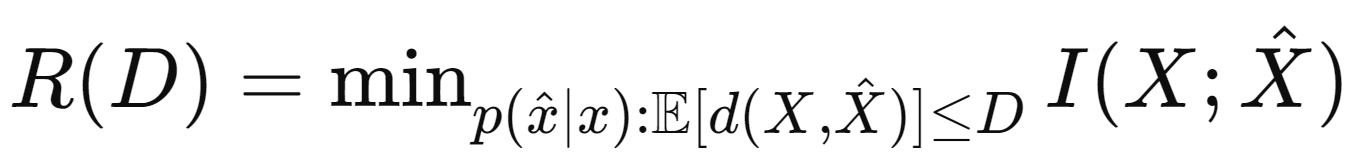
여기서 $R(D)$는 왜곡 $D$에서의 최소 비율을 의미하며 $I(X;\hat{X})$는 원본 데이터 $X$와 복원된 데이터 $\hat{X}$ 간의 상호 정보량
- 모델의 샘플이 고품질이므로, Diffusion 모델이 우수한 손실 압축기를 만들 수 있을 것이다 !
- Equ(5)에서 VB의 각 시간 스텝 t에 대한 손실 항목 $L_t$를 Rate로 해석하고, 데이터를 압축하는 데 필요한 평균 비트 수를 의미 => $L_t$는 모델이 각 시간 스텝에서 데이터를 얼마나 잘 설명하는지를 평가
- VB의 $L_0$ 항목을 Distortion으로 해석하여 압축된 데이터를 원래 데이터로 복원할 떄 발생하는 정보 손실 의미
Progressive lossy compression
이 성능을 평가하기 위해 rate-distortion behavior 조사
$x ~ q(x)$를 약 $D_{KL}(q(x)||p(x))$ bits를 사용하여 샘플링할 수 있는 절차 가정하며 receiver은 오직 p만을 사전에 사용할 수 있음
$x_0 ~ q(x_0)$에 적용할 때, algorithm 3, 4는 Equ(5)에 따라 총 예상 코드 길이를 사용하여 $x_T, ..., x_0$를 전송
Receiver은 각 시간 $t$에서 부분 정보를 기지고 $x_0$를 추정할 수 있음
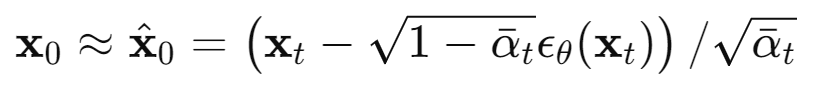
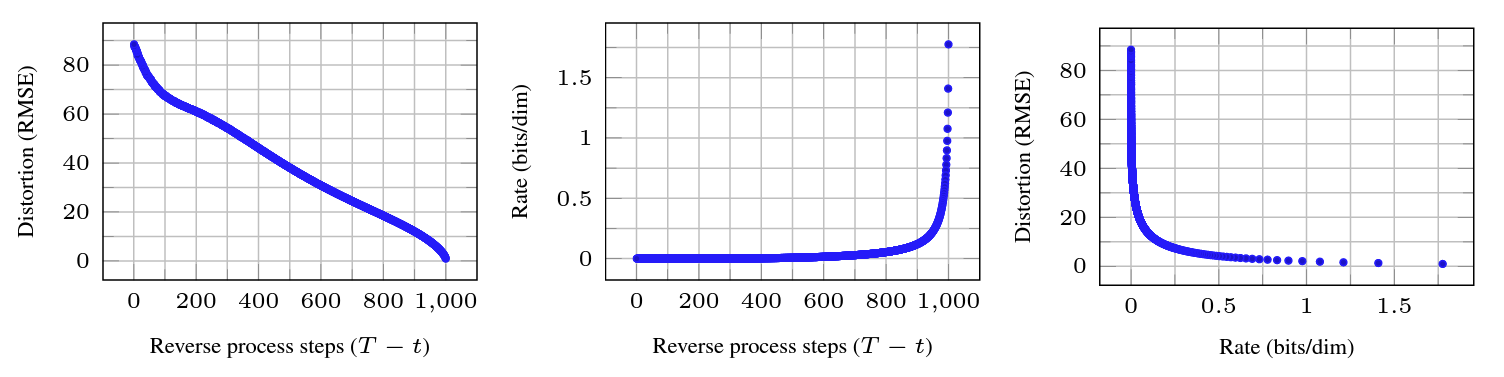
Progressive Generation
무작위 비트로부터의 점진적인 decompression을 통해 데이터를 생성하는 방법
역방향 프로세스를 사용하여 샘플링하면서, 최종적으로 복원된 데이터 $\hat{x}_0$를 예측하는데, 이때 역방향 프로세스를 통해 데이터를 점진적으로 복원하는 알고리즘 2을 이용 (각 스텝 $x_t$에서 모델 $p_\theta(x_{t-1}|x_t)$를 사용하여 이전 상태를 예측)하여 무작위 상태 $x_T$에서 시작하여 점진적으로 $x_0$에 도달

Figure 6은 역방향 프로세스 동안의 샘플 품질을 보여주고, 이미지의 큰 특징은 먼저 나타나고, 세부사항은 나중에 나타난다는 것을 확인할 수 있음
Figure 7에서는 다양한 t 값에 대해 고정된 $x_t$로부터의 확률적 예측을 보여줌 => t 가 작을 때는 모든 세부 사항이 유지되지만, t 가 클 때는 큰 특징만 유지
Autoregressive Decoding
Autoregressive Model
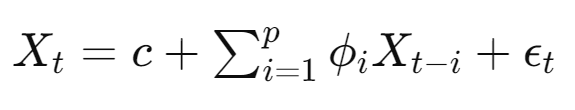
$X_t$: 시간 t에서의 데이처 포인트
$\phi_i$: 이전 i 시점의 데이터 포인트에 대한 가중치 (회귀 계수)
$p$: 모델의 차수 (몇 개의 이전 시점을 사용할 것인지?)
$\epsilon_t$: 평균이 0이고 분산이 일정한 백색 잡음 (오차항)
특징: 모델이 자신의 과거 값을 사용하여 현재 값을 예측하는 자기회귀, 현재 값은 과거 값들의 선형 결합으로 표현, 시계열 데이터가 시간에 따라 통계적 특성이 일정한 경우, AR 모델이 잘 동작하는 정상성 (stationarity)를 가짐

머신러닝에서는 순차 데이터 모델링에서 사용, NLP에서는 이전 단어들을 기반으로 다음 단어를 예측하는 데 사용
VB를 autoregressive decoding과 연결하여 해석 => Gaussian diffusion 모델이 autoregressive 모델과 유사한 방식으로 동작!
VB $L$를 다음과 같이 재작성할 수 있음

여기서,
최종 시간 T에서의 KL divergence |
각 시간 스텝에서의 KL divergence의 기대값 |
$x_0$의 엔트로피 |
Diffusion 과정의 길이 T를 데이터의 차원 수에 맞추고 정방향 과정에서 $q(x_t|x_0)$가 $x_0$의 처음 t개의 좌표를 마스킹하는 방식으로 정의한다고 가정.
$p(x_T)$는 빈 이미지를 나타내며, $p_\theta(x_{t-1}|x_t)$는 fully expressive conditional 분포가 됨
$D_{KL}(q(x_T)||p(x_T)) = 0$, $D_{KL}(q(x_{t-1}|x_t)||p_\theta(x_{t-1}|x_t))$를 최소화하는 것은 $p_\theta$가 $t+1, ..., T$ 좌표를 그대로 복사하고, t번째 좌표를 예측도록 훈련된다는 것을 의미
따라서, 이 특정 diffusion을 사용하여 $p_\theta$를 훈련하는 것은 autoregressive 모델을 훈련하는 것과 같다!
- 재정렬 효과: 이전 연구에 따르면, 이러한 재정렬은 샘플 품질에 영향을 미치는 유도 바이어스(inductive biases)를 도입하여 Gaussian noise는 마스킹 노이즈에 비해 이미지에 더 자연스러울 수 있음
- Gaussian diffusion 길이는 데이터 차원과 일치할 필요가 없음, 실험에서는 T=1000을 사용하며, 이는 32x32x3 또는 256x256x3 이미지의 차원보다 작음. Gaussian diffusion은 빠른 샘플링 또는 모델 표현력을 위해 더 짧게 또는 더 길게 설정할 수 있음
(4) Interpolation
- Source image $x_0, x'_0 ~ q(x_0)$를 잠재 공간에서 보간 → 잠재 공간에서 선형 보간된 잠재 변수 $\bar{x}_t = (1 - \lambda)x_0 + \lambda{x'_0}$
- 역방향 과정을 통해 보간된 잠재 변수를 이미지 공간으로 디코딩 => $\bar{x}_0 ~ p(x_0|\bar{x}_t)$을 통해 이미지를 생성 => 원본 이미지의 왜곡된 버전을 선형 보간한 후, 역방향 과정을 통해 인공물을 제거하는 방식으로 작동
- 다른 $\lambda$ 값에 대해 노이즈를 고정하여 $x_t$와 $x'_t$가 동일하게 유지되도록 함
- t가 커질수록 더 거칠고 다양한 보간이 생성